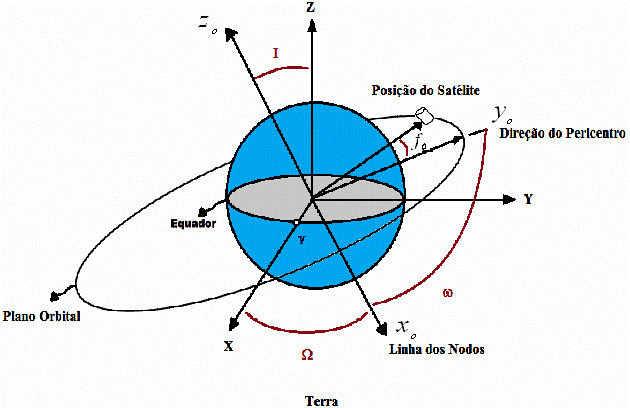
Figura 1: Representação da órbita de um satélite artificial, com os elementos orbitais angulares, sendo z 0 o eixo perpendicular ao plano orbital. (MOTTA, 2011).

Introdução

Os elementos orbitais são seis (6) parâmetros que permitem a realização da análise do movimento orbital de um satélite. Tais parâmetros são obtidos através de três grandezas escalares e três grandezas angulares.

Conhecendo os seis parâmetros e o tempo é suficiente para que se saiba a especificação completa do estado do movimento do satélite.

Com base nos valores destes parâmetros os operados de controlo de satélite efectuam as manobras de correcção orbital. 

Algumas definições

Para que se perceba melhor o assunto em questão, vamos apresentar abaixo as seguintes definições:

Segunda lei de Newton – o somatório das forças que actuam num corpo é igual ao produto da sua massa pela sua aceleração;

Lei da gravitação universal – a força de interação entre dois corpos é directamente proporcional ao produto das massas e inversamente proporcional ao quadrado da distância que os separa;

Primeira lei de Kepler – a órbita de cada planeta é uma elipse com o Sol em um dos focos;

Segunda lei de Kepler – a linha que une o planeta ao Sol varre áreas iguais em intervalos de tempos iguais;

Terceira lei de Kepler – o quadrado do período é direitamente proporcional ao cubo da distância média ao Sol;

Órbita – trajectória descrita pelo satélite durante o seu movimento;

Vector de estado – conjunto de seis (6) componentes três (3) do vector posição e três (3) do vector velocidade. 

Problema dos dois corpos

O problema dos dois corpos trata da interacção gravitacional de um sistema isolado de dois corpos, combinando a segunda lei de Newton com a lei da gravitação universal, e obtendo então a equação de movimento de um corpo em relação ao outro.

Constantes de movimento ou integrais do problema dos dois corpos

Da equação de movimento do problema dos dois corpos, com auxílio de algumas manipulações matemáticas se obtém três (3) constantes h, E e e, onde:

• h – momento angular específico é normal ao plano de movimento;
• E – energia mecânica específica;
• µe – vector de Laplace e aponta para direcção do perigeu;
  • µ – parâmetro gravitacional da terra.

Estas três (3) grandezas são chamadas de constantes de movimento. Elas permanecem invariáveis durante o movimento no caso do sistema de dois corpos isolados. 

Elementos Keplerianos

Elementos Keplerianos são o conjunto de elementos utilizados para descrever órbitas fechadas (Elíptica ou Circular). Também são chamados elementos clássicos orbitais, ou elementos de dois-corpos.

Os elementos Keplerianos são:

• O semi-maior eixo (a), que específica o tamanho da órbita;
• A excentricidade (e), que específica a forma da órbita, e é a magnitude do vector excentricidade, o qual aponta em direcção ao perigeu.
• A inclinação (i), que especificada a inclinação do plano orbita, o qual é definida como o ângulo entre o vector momento angular (), e o eixo OZ positivo.
• (RAAN) a ascensão recta do nó (), é o ângulo do eixo positive OX, IX, para o vector do nodo ascendente, , que varia entre 0 a 2.
  • O nodo ascendente é o ponto no plano equatorial onde a órbita cruza ou separa o pólo sul do pólo norte.
• O argumento do perigeu (), é medido do nodo ascendente para o ponto mais próximo, o perigeu, Pode variar de 0 a .
• A anomalia verdadeira (), específica a posição do satélite dentro da sua órbita, e o ângulo entre perigeu e actual posição do vector (), Pode variar de 0 a :

Os elementos Keplerianos sofrem duas particularidades principais. A primeira ocorre em órbitas circulares, o qual tem excentricidade próxima de zero, e deixa a linha dos ápices indefinida. A segunda ocorre com órbitas equatoriais, qual tem inclinação próxima de zero, e deixa a linha do nó indefinida. 

Resumo

Na determinação do movimento do satélite e de grande relevância os elementos Keplerianos bem como as influências dos campos gravitacionais dos corpos celeste, visto que o movimento do satélite é feito em um plano orbital, e tal plano é uma consequência do campo de força central, estando estes dois critérios sempre conectados.

Referências

1. Richard Harry Lyon. Geosynchronous Orbit Determination Using Space Surveillance Network bservations and Improved Radiative Force Modeling. Massachusetts institute of Technology, 2004;
2. Murray R. Spiegel. Theory and Problems of Theoretical mechanics. McGRAW-HILL, 1982;
3. Jerry Jon Sellers. Understanding Space: An Introduction to Astronautics. McGRAW-HILL, 2004.

Autor

Joaquim Luvuvamo Cardoso Daniel
Especialista em Suporte a Navegação Balística